Wäre die Erde eine Scheibe, könnten wir uns das folgende Kapitel (fast) sparen. Doch wer nach Kopernikus und Galilei immer noch nicht daran glaubt, dass wir auf einer mehr oder weniger idealen Kugel leben, wird spätestens nach dem Anblick der ersten Satellitenbilder von unserem blauen Planeten nicht mehr daran zweifeln!
Um nun ein Stück dieser kugeligen Erdoberfläche als Navigationskarte handhabbar zu machen, müssen wir eine Möglichkeit finden, dasselbe auf einer ebenen Fläche abzubilden. Da man dies nicht ohne Verzerrungen erreichen kann, muss man sich entscheiden, welche Merkmale wichtig sind und möglichst "treu" erhalten bleiben sollen. Daher haben sich im Laufe der Entwicklungsgeschichte zur Herstellung von Navigationskarten mehrere Abbildungsverfahren entwickelt, von denen je nach Verwendungszweck die eine oder andere besser zur Navigation geeignet ist.
Die Lambertsche Schnittkegelprojektion
Im Gegensatz zur echten Kegelprojektion, bei der ein Kegel an einem Breitenkreis die Erde berührt, sind es bei der Schnittkegelprojektion zwei Breitenkreise.
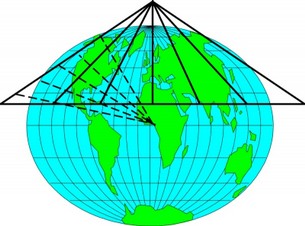
Bildlich gesehen kann man sich die Herstellung einer Karte nach der Kegelprojektion folgendermaßen vorstellen: Man stülpt einen Hohlkegel so über die Erde, dass sich die Kegelspitze in der Verlängerung der Erdachse befindet. Bei der Schnittkegelprojektion dringt dabei der Kegel, je nach gewünschtem Kartenmaßstab, so weit in die Erde ein, dass zwei Breitenkreise, deren Abstand von der Eindringtiefe abhängig ist, den Projektionskegel schneiden. Diese Breitenkreise nennt man die "Bezugsbreitenkreise".
Für die Übertragung der Oberflächenmerkmale der Erde auf den Kegel denken Sie sich im Erdmittelpunkt eine Lichtquelle, die mit einem scharf gebündelten Lichtstrahl die Erdoberfläche von innen heraus abtastet und in dessen Verlängerung auf der Kegeloberfläche abbildet, wie es Abb. 3.1 zeigt. Schneidet man schließlich den Kegel vom Rand zur Spitze hin entlang eines Längengrades auf, erhält man die gewünschte Karte.
Die beiden Bezugsbreitenkreise werden mit dieser Projektion längentreu abgebildet. Die Meridiane (Längenkreise) werden zum Pol hin als Geraden abgebildet, wogegen die Breitenkreise als konzentrische Kreisbögen vorhanden sind. Das Wichtigste für die Navigation und für das Einzeichnen von Kursen in die Karte ist jedoch, dass die Abbildung vollständig winkeltreu ist. Da speziell in der Luftfahrt ein Kurs meist auf einer Orthodrome (einem Großkreis) liegt und diese auf der Karte eine gerade Linie bildet, wird die Lambertsche Schnittkegelprojektion vorzugsweise in der Flugnavigation verwendet. Die Orthodrome ist dabei die Linie, die zwei Punkte auf einer Kugel durch den kürzesten Weg miteinander verbindet.
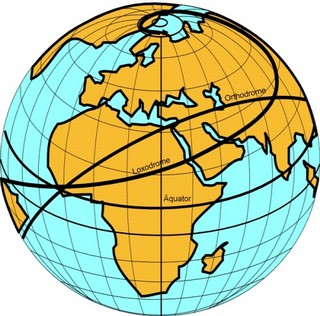
Der Vollständigkeit halber sei hier noch im Gegensatz zur Orthodrome die Loxodrome erwähnt. Hierbei handelt es sich um eine weitere Linie, welche die Längenkreise (Meridiane) immer unter demselben Winkel schneidet. Daher bewegt sie sich spiralförmig auf die beiden Pole zu (Abb. 3.3).
Die Zylinder- oder Mercatorprojektion
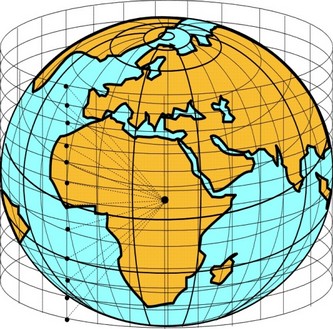
Für die Herstellung einer Karte nach der Zylinder- oder Mercatorprojektion stülpt man einen Zylinder so über die Erde, dass die Innenfläche dieses Zylinders diese genau am Äquator berührt. Die Oberflächenmerkmale der Erde denkt man sich wiederum als Achsenverlängerung eines vom Erdmittelpunkt kommenden Lichtstrahls auf die Zylinderoberfläche projiziert. Nach dem Aufschneiden des Zylinders erhält man eine winkeltreue Karte mit parallellaufenden Breitenkreisen, deren Abstände sich vom Äquator aus zu den beiden Polen hin vergrößern. Die bereits erwähnte Loxodrome erscheint hier als eine gerade Linie, deshalb sind Mercatorkarten bevorzugte Seenavigationskarten.
Für die Landvermessung und für die Navigation in der Polargegend dreht man den Projektionszylinder um 90o gerade so, dass die Innenfläche einen Meridian berührt. Diese Projektion nennt man dann Transversale-Mercator-Projektion.
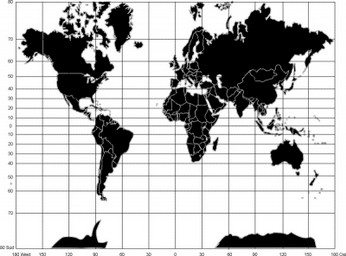
Die Meridiane erscheinen bei dieser auf dem Zylinder und somit dann auch auf der resultierenden Karte als gerade Linien und die Breitenkreise sind, mit Ausnahme des Äquators, gebogen. Abb. 3.5 zeigt eine winkeltreue Projektion nach Mercator.
Azimutalprojektionen
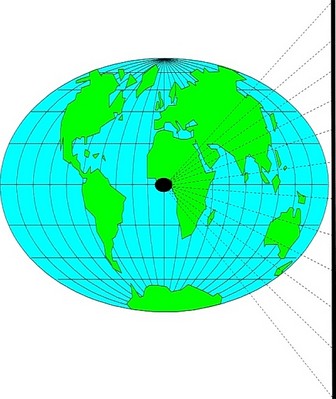
Eine weitere Gruppe von Kartenprojektionen sind die Azimutalprojektionen. Von diesen findet überwiegend die Gnomonische Projektion, bei der alle Großkreise als gerade Linien abgebildet werden, in der Navigation Verwendung. Die Projektionsebene ist dabei eine beliebige Fläche, deren Berührungspunkt mit der Erde in das Gebiet gelegt wird, das später auch den Mittelpunkt der Karte bilden soll. Da die Orthodrome hier eine gerade Linie bildet, wird diese Karte hauptsächlich für die Großkreisnavigation verwendet. Sowohl die Breitenkreise als auch die Meridiane haben ungleiche Abstände, wobei nur die Meridiane parallel und gerade verlaufen.
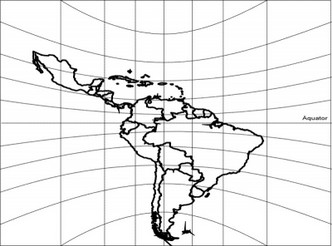
Abb. 3.6 zeigt die äquatorständige gnomonische Projektion. Der Berührungspunkt der Tangentialebene liegt am Äquator und das Projektionszentrum ist wiederum der Erdmittelpunkt. Das Ergebnis solch einer Projektion, bei der als Beispiel der Berührungspunkt über Lateinamerika liegt, zeigt die Kartenskizze nach Abb. 3.7.
Nun wissen wir also, wie unsere gute alte Erde in eine handliche, zusammenklappbare Form gebracht werden kann, damit wir diese als Navigationskarten (doch bequemer als einen Globus) in einem Land-, Luft- oder Wasserfahrzeug mitführen können. Als nächstes gilt es nun, jedem Punkt auf diesen Karten und damit auf der Erdoberfläche eine individuelle "Adresse" zuzuordnen.
Terrestrische Koordinatensysteme
Auch hier gibt es (wie könnte es auch anders sein) wieder verschiedene Möglichkeiten und Versuche, einen bestimmten Punkt oder eine bestimmte begrenzte Fläche eindeutig zu bestimmen.
Es gibt Anwendungen, bei denen nicht der einzelne Punkt selbst wichtig ist. Vielmehr genügt es, eine Fläche anzugeben, innerhalb der sich dieser Punkt befindet. Das GEOREF-System z.B. teilt die Erdoberfläche in Vierecke von jeweils 15 Grad ein, wobei jedes Viereck nochmals in 1 Grad - Felder unterteilt wird. Jedes Feld wird durch eine Kombination von zwei Buchstaben beschrieben, die bei den großen Feldern am Südpol mit "AA" beginnen und in Ost- und Nordrichtung verlaufend am Nordpol mit "ZM" enden. Die Bezeichnung der einzelnen 1 Grad - Felder beginnt ebenfalls in der südwestlichen Ecke mit "AA" und endet in der nordöstlichsten mit "QQ". Solche und ähnliche Koordinatensysteme werden für den Aufbau von Meldesystemen, Funknetzzellen oder bei den Amateurfunkern als QNH-Locatoren (Antennenstandortflächen) benützt.
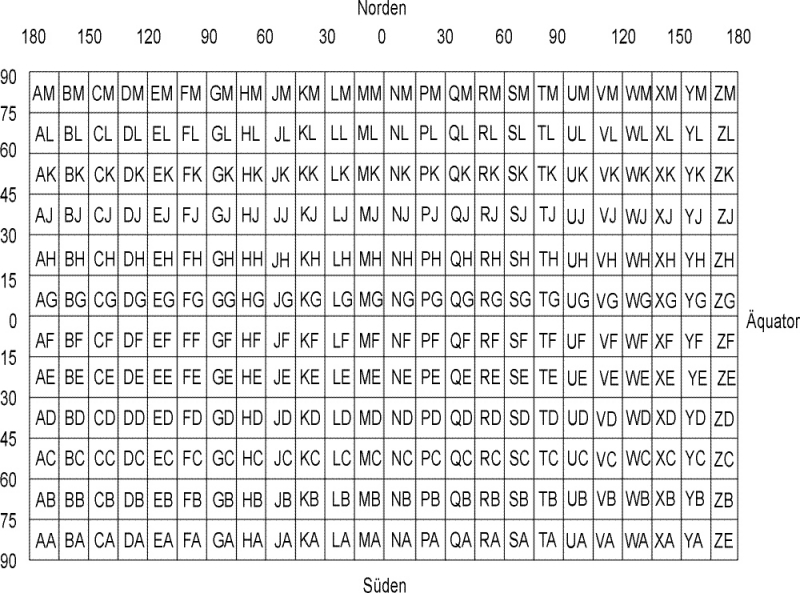
Tabelle 3.1 Die Erdoberfläche nach GEOREF
Auch das UTM-System (UniversalTransversalMercator -System), welches auf der schon oben beschriebenen transversalen Zylinderprojektion basiert, ist ein Meldesystem mit 100 km großen Quadraten und alphabetischer Zellenbezeichnung. Da die Breitenkreise bei der Mercatorkarte als gebogene Linien abgebildet werden und die Größe der Zellen konstant ist, entstehen entlang der Meridiane unterschiedlich große Restzellen, die extra bezeichnet werden müssen.
Für die Navigation und die Erstellung von Navigationskarten hat sich jedoch ein Gradsystem mit geographischen Koordinaten durchgesetzt, da die Genauigkeit der Ortsbestimmung mit Systemen wie GEOREF und UTM (es gibt noch einige mehr davon für spezielle Zwecke) für ein präzises Navigieren bis hin zur Landung von Flugzeugen bei Sicht Null nicht ausreichend ist. Dieses System lässt sich am einfachsten an der flächentreuen Abbildung der Erde erklären.
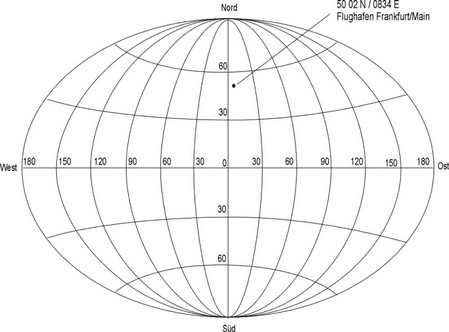
Man benützt als Referenz zwei rechtwinklig zueinander liegende Flächen, die durch Großkreise begrenzt sind. Der eine Großkreis geht durch die beiden Pole und durch Greenwich (England), der andere bildet den Äquator. Der Kreuzungspunkt des Äquatorgroßkreises mit dem Greenwich-Meridian ist der geographische Nullpunkt aller Ortsangaben. Von hieraus ist es möglich, jeden Punkt auf der Erdoberfläche durch Angabe von nur zwei Winkeln (Phi j für die geographische Breite und Lambda l für die geographische Länge) zu beschreiben. Um Zweideutigkeiten auszuschließen und keine Vorzeichen für die Gradangaben benützen zu müssen, werden den Koordinaten die Buchstaben N (Nord oder North), S (Süd oder South), W (West) oder O (E) für Ost (bzw. East) zugefügt.
Abb. 3.9 zeigt einen Ausschnitt aus einer ICAO-Luftfahrtkarte für die Sichtflugnavigation im Maßstab 1:500.000. Durch das überlagerte Gitternetz lassen sich die gewünschten Orte in der Karte sehr genau herausmessen. Um die eigentlichen Geländemerkmale nicht mit Koordinatenstrichen zu übersäen, ist eine Rasterung von zehn Bogenminuten vorgesehen. Jede Minutenkoordinate ist weiter unterteilt, so dass zwei benachbarte Minutenkoordinatenlinien bequem mit einem Lineal zur Auswertung miteinander verbunden werden können.
Acht solche Luftfahrtkarten mit den Bereichen Hamburg, Rostock, Hannover, Berlin, Frankfurt, Nürnberg, Stuttgart und München in der Größe von etwa DIN-A1 sind für die Sichtflugnavigation erhältlich.
Leider ist das Einzeichnen von Längen- und Breitenkreisen in den Straßenkarten, wie Sie für den Autofahrer angeboten werden, sowie in den Atlanten noch unüblich. Dies dürfte sich jedoch nach der globalen Einführung der Satellitennavigation schlagartig ändern.
Inzwischen werden von verschiedenen Kartenverlagen bereits Compact-Disks mit digitalisierten Straßenkarten angeboten. Diese Karten können auf den Bildschirmen handelsüblicher Personalcomputer in den verschiedensten Maßstäben ausgegeben werden. Ausgeklügelte Programmroutinen berechnen dabei dem Autofahrer auf Wunsch die kürzeste Entfernung zwischen zwei Orten und die voraussichtliche Fahrtdauer nach der eingegebenen Durchschnittsgeschwindigkeit. Da solche Systeme bereits Schnittstellen für die Dateneinspeisung von GPS-Signalen erhalten, werden sie zur Navigationsvorbereitung und -durchführung in naher Zukunft ihren Einzug feiern können.
Bei den bisher besprochenen Koordinatensystemen handelt es sich um zweidimensionale terrestrische Systeme. Für die Satellitennavigation benötigen wir jedoch ein dreidimensionales, da wir hier außer Längen- und Breitengrade auch noch die Höhen und damit Raumpositionen erhalten.
Astronomische Koordinatensysteme
Die optische Astronomie war bis zur Einführung des ersten Satellitennavigationsystems mit der Bezeichnung TRANSIT die einzige Möglichkeit, die Position eines Punktes auf der Erdoberfläche dreidimensional zu bestimmen. Man stelle sich als Himmelskugel eine Hohlkugel mit unendlich großem Durchmesser und unserer Erde als Mittelpunkt darin vor. Die Verlängerung der Erdachse bezeichnet man als die Himmelsachse. Die Ebene des Erdäquators deckt sich mit dem Himmelsäquator, da der Durchmesser der Himmelskugel unendlich groß ist und der Durchmesser der Erde damit vernachlässigt werden kann.
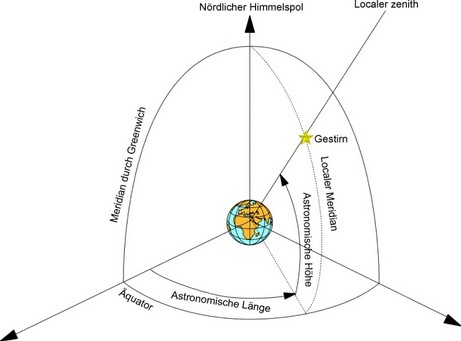
Die Ortsangabe eines Gestirns erfolgt mit zwei Winkelwerten, der Elevation (Höhe) über dem wahren Horizont (0 bis 90 Grad) und dem Azimut (Bogen auf dem Horizont). Da sich die Erde dreht und die Gestirne dabei scheinbar am Himmel einen Bogen beschreiben, muss zur Positionsbestimmung eine exakt funktionierende Uhr zur Verfügung stehen. Aus Tabellen oder aus Karten lassen sich zu ganz bestimmten Zeiten für ausgewählte markante Gestirne die Daten für eine Ortsbestimmung ablesen.
Für eine präzise Positionsbestimmung wird die astronomische Position heute so gut wie nicht mehr benützt. Lediglich zum Studium der Gravitation und zur Messung der vertikalen Veränderung der Erdoberfläche, weitestgehend historisch bedingt, findet sie noch Ihre Verwendung.
Das WGS-84 (World-Geodetic-System 1984)
GPS-Navigation kann auf sechs Arten betrieben werden, je nachdem wie die Daten und Übertragungsarten, die zur Verfügung stehen, ausgewertet werden. Jeweils drei dieser Arten gehören zu den beiden Hauptvermessungskategorien: absolute und differentielle Navigation.
Für das Verständnis der absoluten Satellitennavigation genügt uns das astronomische Koordinatensystem, das auf dem WGS-84 (World Geodetic System 1984) aufbaut. Es bildet die Koordinatengrundlage für das amerikanische NAVSTAR-Konzept. Die differentielle Navigation ist sehr viel präziser als die absolute, jedoch auch sehr viel aufwendiger und für den Anwender auch nicht mehr autark auszuführen. Über die Differentialnavigation erfahren Sie später mehr. Zunächst möchte ich mich der absoluten Navigation widmen. Dafür ist das WGS-84 das grundlegende Koordinatensystem für das NAVSTAR-GPS-Konzept. GLONASS, das russische Äquivalent, baut auf dem SGS-85 Koordinatensystem auf.
Die Erde ist keineswegs eine ideale Kugel. Das WGS-84 Koordinatensystem ist deshalb ein spezifisches dreidimensionales Koordinatensystem mit dem Koordinatenursprungspunkt im Massezentrum eines der gesamten Masse der Erde angenäherten Ellipsoids mit einer angenommenen Haupthalbachse von 6.378.137 m.
Die positive X - Achse geht von dessen Massezentrum durch den Schnittpunkt von Äquator und Greenwich-Meridian. Die Y - Achse liegt in derselben Ebene und verläuft, 90 Grad zur X - Achse, ebenfalls durch den Äquator. Die Z - Achse bildet die dritte räumliche Koordinate und geht durch den geographischen Nordpol. Ein Ort auf der Erdoberfläche, der hier wie bei den terrestrischen Koordinatensystemen mit Phi und Lambda festgelegt wird, erhält jetzt noch eine dritte Koordinate, die Höhe h.
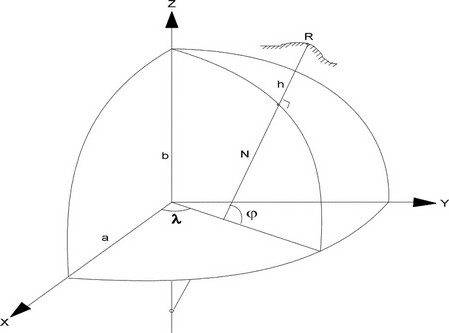
Jeder Vektor in diesem terrestrischen System kann durch kartesische Koordinaten (X, Y und Z) oder durch elliptische (j, l und h) beschrieben werden. j entspricht dabei dem Breitengrad (engl.: Latitude), l dem Längengrad (engl.: Longitude) und h der Höhe. In der Abbildung 3.11 bezeichnet N den Radius der Erdkrümmung für den entsprechenden Ort, a die größte Halbachse und b die kleinste für das angenommene Ellipsoid.
Für die absolute Position eines Ortes in diesem System interessieren den Navigator drei Werte: die geographische Breite zwischen 90 Grad Nord und 90 Grad Süd, die geographische Länge zwischen 180 Grad Ost und 180 Grad West und die Höhe über dem Meeresspiegel. Um diesen Ort aus den Signalen der Navigationssatelliten zu berechnen (bei der Höhe interessiert dabei nicht die Höhe über dem Erdmittelpunkt, sondern die über dem mittleren Meeresspiegel), sind umfangreiche Koordinatentransformationen nötig, die je nach der erforderlichen Genauigkeit mit mehr oder weniger Aufwand über Iterationen oder Näherungsformeln vom GPS-Navigator ermittelt werden müssen.
Diese Umrechnungen, die tief in die Mathematik gehen, sollen hier nicht weiter interessieren. Für den Anwender von GPS-Navigatoren ist es nur wichtig zu wissen, dass für das NAVSTAR-GPS das WGS-84 Koordinatensystem bei der Personalisierung des GPS-Empfängers eingegeben werden muss bzw. es muss überprüft werden, ob diese Einstellung vom Hersteller nicht bereits schon vorgenommen wurde. Die meisten Geräte bieten nämlich die Möglichkeit an, noch andere Koordinatensysteme als Referenz zu wählen. Beim Garmin 55 sind es z.B. über 100! Ein falsch gewähltes Koordinatensystem kann Positionsfehler von mehreren hundert Metern hervorrufen.
